
Ten Equations that Change the World
The brightest mind in history have used mathematics to lay the foundation for how we measure and understand our universe. Time and time again, we have proved that it only takes one simple formula to alter the course of humanity. Here are ten equations that did just that.
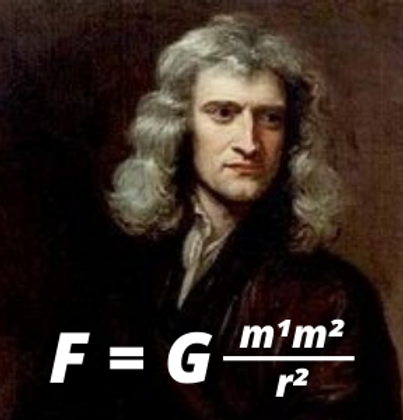
1. Isaac Newton's Law of Universal Gravitation
Newton's Law explains why the planets move the way they do, and how gravity works, both on earth and throughout the universe. First published in the The Principia in July 1687, the Law of Universal Gravitation was the defacto reference equation for nearly 200 years until Einstein's Theory of General Relativity replaced it.
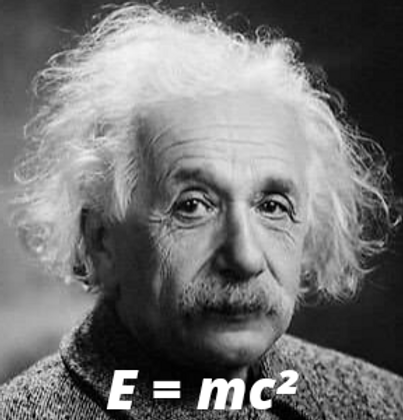
2. Albert Einstein's Theory of Relativity
Einstein's most famous undertaking is the generally accepted theory on the relationship between space and time. First proposed in 1905, the Theory of Relativity has both radically altered the course of physics, and deepend our knowledge of the universe's past, present and future.
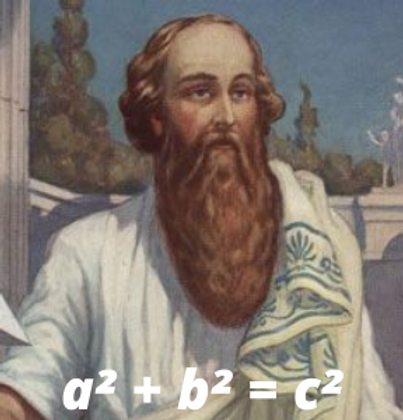
3. The Pythagorean Theorem
The ancient theorem - first recorded circa 570-495 BC -- is a fundamental principles in Euclidean Geometry, and the basis for the definition of distance between two points. Phythagoras' theorem also describe the relationship between the sides of a right triangle on a flat plane.

4. Maxwell's Equations
James Clerk Maxwell's set of equation describe how electric and magnetic fields are regenerated and altered, both by each other and by charges and currents. First published between 1861 to 1862, they are to classical electromagnetism what Newton's Law of motion and universal gravitation are to classical mechanism.

5. The Second Law of Thermodynamics
Rudolf Clasius' law states that energy always flow from higher concentration to lower concentration. It also states that whenever energy changes or moves, it becomes less useful. Formulated in 1865, it has led to the development of technologies like internal combustion engines, cryogenics, and electricity generation.
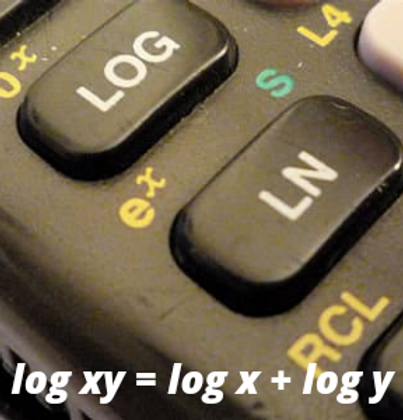
6. Logarithms
Logarithms were intoduced by John Napier in early 17th century as a way to simplify calculations. They answer the questions, "How many of X number do we multiply to get Y number?". Logarithms were adopted by early navigators, scientist and engineers. Today, scientific calculators and digital computers do the work for us.

7. Calculus
The calculation shown in the definition of the derivative in differential calculus, one of calculus' two major branches. The derivatives measures the rate at which quantity is changing--if you are walking 2 km an hour, then you will change your position by 2 km every hour. In the 1600s, Newton used calculus to develop his laws of motion and gravitation.

8. Schrõdinger's Equation
This equation describe how the quantum state of quantum system changes with time. Developed by Austrian physicists Erwin Schrõdinger in 1926, it governs the behavior of atoms and subatomic particles in quantum mechanics. Schrõdinger's Equation paved the way for nuclear power, microchips, electron microscopes and quantum computing.

9. Information Theory
Information theory is a branch of mathematics that studies the coding of information in the form of sequences of symbol, at the speed at which that information can be transmitted. Application of topics within information theory include the date compression and channel coding. Research in the field was also instrumental in the development of the internet and mobile phones.
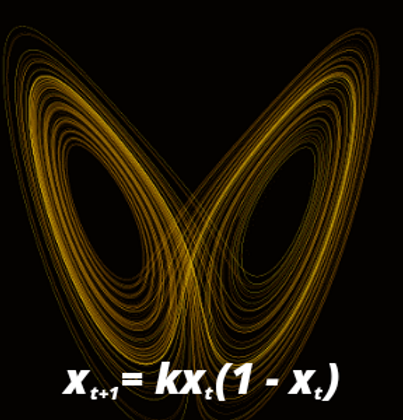
10. Chaos Theory
Chaos Theory is a branch of mathematics that studies complex system whose behavior is extremely sensitive to slight changes in conditions. In essence, it shows how small alterations can lead to consequences of much greater scale. Chaos Theory has application just about everywhere--meteorology, sociology, physics, computer science, engineering, economics, biology, and philosophy.